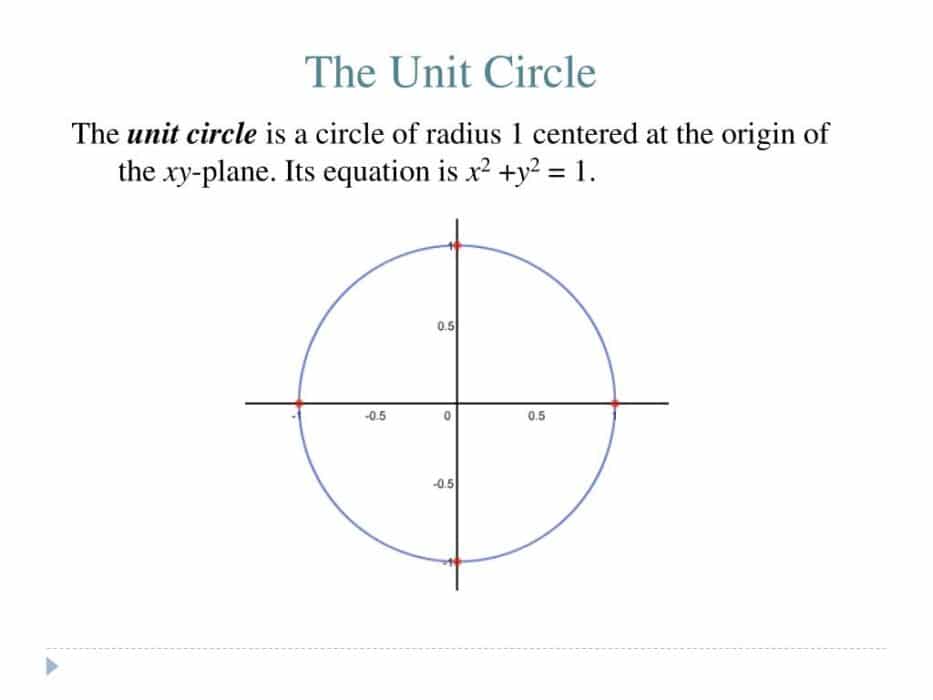
In mathematics, the concept of the unit circle is a sort of circle that has a unit radius. You already know that the unit radius means having a value of 1. You can say that, in the trigonometry, the unit circle is the type of circle with unique value. The value at the origin of the circle is centered as (0, 0). Learn More about Trig Identities with us.
Understand the values of the Unit circle:
The value is granted in the Euclidean plan for the Cartesian coordinate system. In the latest mathematics topology, the value is denoted as S1. The reason is that most circles are multi-dimensional well; the unit circle in trigonometry is a one-dimensional unit that has n-sphere.
The two-axis are the circle lengths of a triangle that has a value of 1. In this manner, by the Pythagorean hypothesis, x and y fulfill the equation stated as x2 + y2 = 1. You can say that x2 = (-x) 2 for the all values of x.
The impression of any point on the unit will show on the x and y-axis of the circle. These values present in the unit circle. The above position holds all axis (x, y) range on the unit circle. The values are not only located in the primary quadrant. All set of triangle values are different in four quadrants. The inside section of the circle is known as the open unit plate. It is known as the closes unit base.
One may likewise utilize different thoughts of “separation” to characterize other “unit circles.” It may include the Riemannian circle to evaluate the numerical standards for extra models that work in different scientific fields.
Functions of Trigonometric on the Unit Circle:
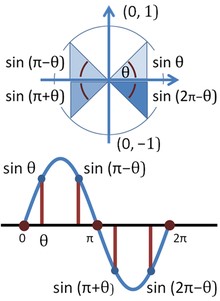
The functions of the trigonometric circle are cosine and sine of edge θ. The values might be characterized by the unit circle as follows. You can makes an edge θ from the x-axis to y with equation x2 + y2 = 1. The unit circle shows sine and cosine are periodic functions. They come up with the characters for any whole number “k”.
The total of the trigonometric elements of the point θ can be developed geometrically as compared to the unit circle, mainly focused at 0 levels. The features of the trigonometry scale work on the unit circle at the top and its chart on the bottom side.
You can say that the triangles are likewise be utilized to symbolize the periodicity of the trigonometric functions. At the first stage, you have to make a length with the name OA. The line originated from the source to a point P(x1, y1). It crosses the unit circle to such an extent to an edge t. The line can be 0 < t < π/2 and shaped with the positive axis of the x-hub. Directly consider a point named with Q(x1, 0). In simple ways, make line fragments with the name PQ ⊥ OQ. You will get the resultant value of the triangle △OPQ. The value of the triangle is t.
Now simply make a line on sin (t) = y1 and cos(t) = x1. If you set up the angle equivalences, then take extra line with the name OR from the center point 0 to a point R (−x1, y1). It seems to look like a similar edge framed on the negative side of the x-axis.
Working with the right kind of triangles, sine, cosine, and all other accessible trigonometric capacities work well with edge quantifies. The values can exceed more than zero and not exactly π/2. Be that as it may, when characterized with the unit circle, these capacities produce essential qualities for any genuine esteemed point measure – even those more prominent than 2π. Do you know that there are standard trigonometric functions? These are sine, cosine, tangent, and their reciprocals are cotangent, secant, and cosecant.
These look similar to versine and exsecant. All functions can be characterized geometrically as far as a unit circle appears on the right side. Using the trigonometry unit circle, for some points other than those labeled determined without using a scientific calculator to get the exact quantity.
Guide to find out the axis values of the unit circle
You can easily find out the axis values by following simple steps. The unit circle is a circle that has a unique radius of 1. The radius of the unit circle with value 1 indicates a straight line. The line is drawn from the middle point of the circle. The length of that line will consistently scale to value 1. Normally, the inside purpose of the unit circle is the place the x and y-axis cross, or at the directions (0, 0).
The unit circle is valuable to know since it lets us effectively ascertain the cosine, sine, and digression of any edge somewhere in the range of 0° and 360°.
As we see in the above graph, by drawing a range at any edge, you will make a correct triangle. The cosine is the level line of the unit circle, and the sine in the unit circle is the vertical line. The triangle’s longest queue, which is known as hypotenuse, is the one that has a value of 1.
So do you think that what are the reasons for the circle popularity? The reason is that you can find out the axis values by using equation a2+b2=c2. With the use of this equation, the symbols a, b, and c are the length, sides, and hypotenuse of the unit circle. We understand that the cosine of any edge is identical to the length of the level circle line. Then again, the sine is proportional to the length of the vertical line. At long last, the hypotenuse is proportional to 1 worth. You can basically get the estimations of the unit hover by following the condition:
cos2θ+sin2θ=1
Continuously recall that these characteristics can be negative depending on the edge formed and what quadrant the two-axis x-and y-falls.