Triangles

A triangle is simply defined as a three-sided polygon that consists of three sides (also known as edges) and vertices. Triangles are  any closed figure in geometry.

Denotation

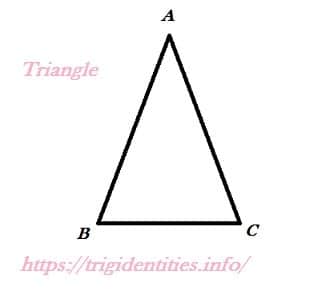
Triangle

Consider a triangle with its vertices A, B, and C, as shown in the above figure. It is denoted as △ABC.

Angles in a triangle

A triangle is of two-dimensional shape with its three-sided polygon. It has three sides, and all the sides are made of straight lines.

The common point where two straight lines of a triangle meet are called a vertex. That is why a triangle consists of three vertices. Each vertex in a triangle forms an angle.




As we know that there are three vertices in a triangle, and each vertex forms an angle in a triangle. Hence, a triangle has three angles, and each angle of a triangle meets at a common point (vertex).

Types of angles

●      Interior angles

In simple words, if an angle lies in the interior of a triangle, then it is called an interior angle. A triangle has three interior angles. The sum of all interior angles of the triangle is equal to 180 degrees.

●      Exterior angles

If we extend any side of a triangle outwards, then it forms an exterior angle with the line. The sum of consecutive exterior and interior angles of a triangle is supplementary, which means it is equal to 180 degrees.

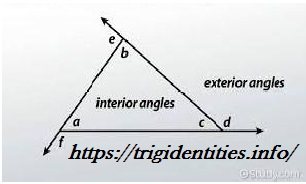
Example of interior and exterior angles

Interior angles

In the figure shown above:

  • b, a, and c represents the interior angle
  • e, f, and d represents the exterior angle

The consecutive sum of e and b, a and f, or c and d will be supplementary.

Properties of a triangle

Every polygon in mathematics has some unique and distinguished properties, making it stand out from the rest. A triangle also has these properties, which are as follows:

  • Every triangle consists of three angles and three sides.
  • The sum of the exterior angle of a triangle is always equal to 360 degrees.
  •  Sum of the interior angle of a triangle is always equal to 180 degrees.
  • The sum of any two sides of the triangle would be greater than the third side.
  • The difference between any two sides of a triangle would be less than the third side.
  • The longest side of any triangle will always be opposite to the largest interior angle.
  • The shortest side of a triangle is always opposite to the sharpest internal rise.
  • The perimeter of the triangle is the sum of its three sides.
  • The area of the triangle is the inner region enclosed by three sides of a triangle.




Types of triangles

A triangle is divided into different types based on its sides and angles. The triangle is divided into 3 types based on its sides, including; equilateral triangles, isosceles, and scalene triangles. On the other hand, triangles can be defined into four different types: the right-angles triangle, the acute-angled triangle, the obtuse angle triangle, and the oblique triangle.

Triangle Based on the sides

There are three types of triangles based on their sides.

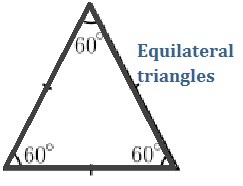
1.     Equilateral triangles

A triangle whose all sides and angles are equal is called an equilateral triangle.

An equilateral triangle is also known as a regular polygon. In an equilateral triangle, the measure of each curve is 60 degrees.

Equilateral triangles

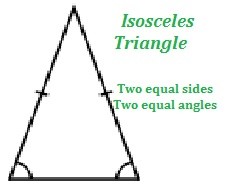
2.     Isosceles triangle

An isosceles triangle is one which has two sides of equal length and one side of unequal length.

An isosceles triangle has two angles of the same measure and one angle of unequal measure. The angles opposite to the equal sides are of equal measure. The angles opposite to the unequal side are of unequal measure.

 

Isosceles Triangle

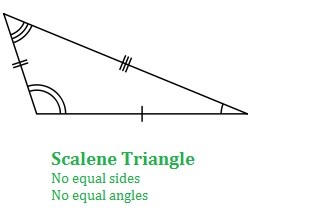
3.     Scalene triangle

An angle whose all sides are unequal in length is called a scalene triangle.

Similarly, as all the sides are unequal in length, so the angles are also unequal in measure.

Scalene triangle

Triangle Based on internal angles

There are six types of triangles based on their inner angles, which are as follows:

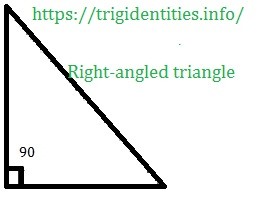
1.     Right-angled triangle

A triangle with one of the interior angles as 90 degrees (right angle) is called a right-angled triangle.

Right-angled triangle

There are some particular properties of right-angled triangles such as:

  • The side opposite of the right angle of a triangle is called the hypotenuse.
  • Right-angled triangles obey Pythagoras theorem (square of the length of the hypotenuse is equal to the sum of the square of the lengths of the other two sides of the triangle)

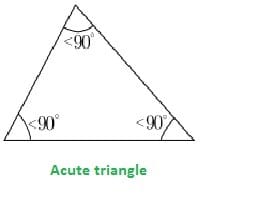
2.     Acute angle triangle or acute triangle

A triangle with all interior angles of measure less than 90 degrees is called an acute angle triangle.

For instance, an equilateral triangle can be an acute triangle as all the measures of angle are less than 90 degrees.

Acute triangle

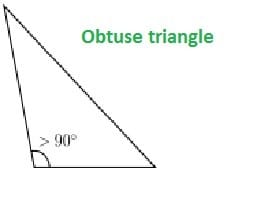
3.     Obtuse angle triangle or obtuse triangle

A triangle with at least one of its angles greater than 90 degrees is called an obtuse-angled triangle.

For instance, a scalene triangle can sometimes be an obtuse triangle if its angles are greater than 90 degrees.

obtuse triangle

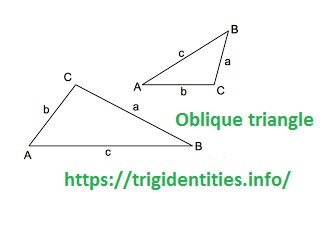
4.     Oblique triangle

A triangle that doesn’t have any of the angles measuring 90 degrees is called a diagonal triangle.

Acute and obtuse triangles can be an oblique triangle as they don’t have any angle equal to 90 degrees.

Oblique triangle

 

Learn more about Trig identities