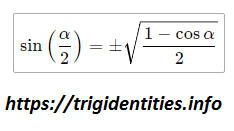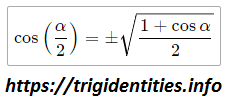Trig Half-Angle Identities

Trig half angle identities or functions actually involved in those trigonometric functions which have half angles in them. The square root of the first 2 functions sine & cosine either negative or positive totally depends upon the existence of angle in a quadrant. Learn more about Trig Identities at trigidentities.info.

Here comes the comprehensive table which depicts clearly the half-angle identities of all the basic trigonometric identities. Explore more about Inverse trig identities.

Derivation of Trig Half-Angle Identities

Today we are going to derive following trig half-angle formulas.

Half Angle Formula – Sine

• cos 2θ = 1− 2sin2 θ

Now, if we let

• θ = α/2

then 2θ = α and our formula becomes:

• cosα=1−2 sin2(2α )

We now solve for

• Sin (α/2)
• 2 sin2(2α )=1−cosα
• sinˆ2 (2α) = 1 – cosα

Solving gives us the following sine of a half-angle identity:

Now let talk about the positive or negative sign of Sin (α/2).

1. If the angle lies in the first quadrant then all positive means sine half angle identity will be positive.
2. And if it is in 3^rd or 4^th quadrant we will introduce a negative sign with the sine half angle identity.

Half Angle Formula – Cosine

Simply by using a similar process, With the same substitutions, we did above. Now we have to substitute these values into the following Trig identity.

• cos 2θ = 2cos² θ – 1

After substituting the values We

• Cosα = 2 cosˆ2(α/2)-1  —–(1)

Now you need to reverse the equation.

Reverse the equation:

• 2 cosˆ2(α/2)-1 = Cosα —–(2)

Add both eq (1) & (2)

• 2 cosˆ2(α/2) = 1+cosα

Divide by 2 on both sides

• cosˆ2(α/2) = 1+cosα/2

Taking square root on both sides we got cosine half angle formula now

let’s talk about the positive or negative sign of Cosine (α/2).

• If the angle lies in first or 4th quadrant then Cosine(α/2) will be positive
• And if it is in 2^nd or 3^rd quadrant we will introduce a negative sign with the cosine half angle identity.