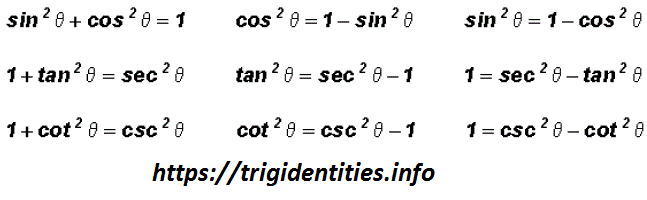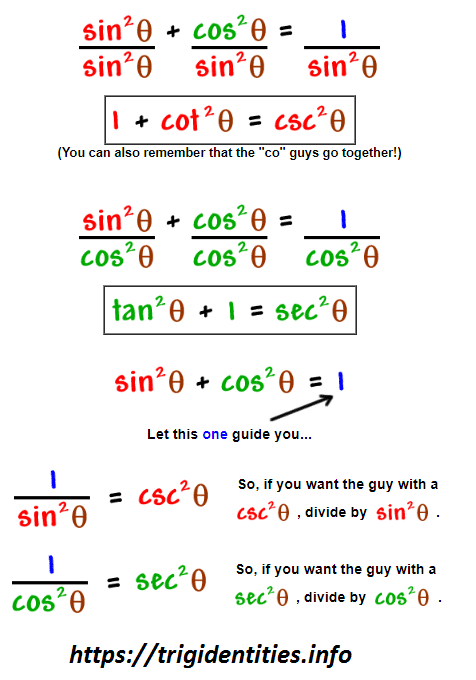Pythagoras Trig Identities are the trigonometric identities which actually the true representation of the Pythagoras Theorem as trigonometric functions. So, these identities help us to fundamentally decide the relationship between different sine, cosine, and tan trigonometric function. From that point, you can determine the function of other trig identities in our lives and how they make our life simple & easy. of life too. Learn more about Trig Identities.
Definition of Pythagoras’ Theorem
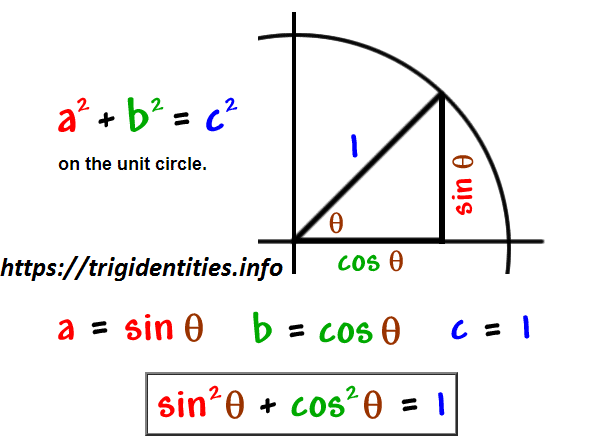
Pythagoras’ Theorem
“For any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”
a2 + b2 = c2
The key Pythagorean Trigonometric identity is:
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
So, from this recipe, we can infer the equations for different capacities additionally:
Recall of Pythagoras Theorem
You are going to need to rapidly review the three Pythagorean Identities. The first Trig Identity of Pythagoras Theorem is very simple and easy to remember because it is Pythagoras Theorem itself.
But is it possible for you to remember the rest of the two? If not then here comes a quick way to drive the rest of 2 from the first equation.