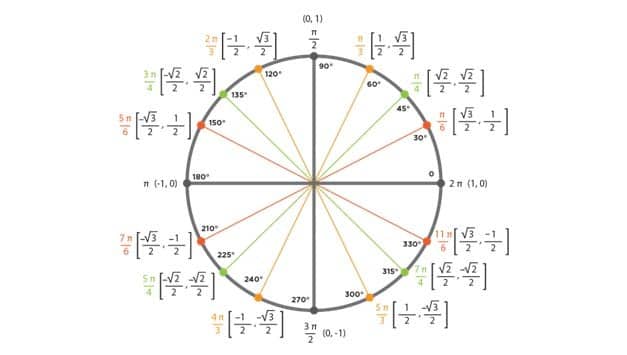
Unit Circle Chart – In mathematics branch trigonometry, a unit circle exists which has a radius of 1. It has a unique value as compared to other circles and curved shapes. It is a circle with a radius one that is centered at the origin spot with values (0, 0). The primary purpose of this unit circle is that it makes other functions of mathematics easier. For example, in trigonometry, the unit circle at any angle uses the value of cosine and sine. The values can be used with sin (θ) = y and cos(θ) = x, which are unique. At the center point, certain angles have the same trig values. Learn more about Unit Circle & Trig Identities with TrigIdentities.info.
The half-unit circle equals 2π. It is an arc of the circle that has an equal length. You can get it when measuring the angle that intercepts this middle arc with a value of 2π as we know that the unit circle radius is one, which is why trigonometric functions have unique values for the unit circle.
Unit Circle Angles in Unit Circle Chart:
In a unit circle, you measure the positive sides of the circle by utilizing the first side of the positive x-axis. At that point, you will instantly move to the terminal side of the circle. The unit circle chart shows the positive points named in radians and degrees.
The terminal sides of the circle angle are structured with a straight line. A few instances of these edge estimations are 30 and 210-degrees, 60 and 240-degrees, etc. The straight lines in the circle measure with 180-degree value. When you analyze the trigonometry circle chart, you will be able to get the values of each angle in four different quadrants.
Understanding the Specifics of the Unit Circle chart:
At the point when you’re working on the trigonometry, you can utilize a unit circle chart. Truth be told, it’s probably the best branch of mathematics that you can utilize. You can quickly download a unit circle in a printed form. It is an easy approach to use the values. You can even make your own unit circle chart. If you comprehend this idea, then trigonometry will turn into significantly simpler.
Before you can get it, you should initially understand the original chart. The unit circle is a sort of circle, which has a sweep of 1. You can utilize this chart to discover exceptional trigonometric ratios and functions.
You can likewise utilize it to assist you with plotting different angle graphs. There’s additionally a number line folded over the unit circle. It may works as an input value chart while accessing the trigonometry functions.
The idea of 6 basic trig ratios in a unit Circle
In the unit circle chart, there are different ratios exist. All the ratios have different values and functions. The chart has Sin, Sec, Tan, Cos, Csc, and cot ratios. If you want to analyze the while chart easily, you should remember their functions as well. The ratios are:
- sinθ = opposite/hypotenuse
- tanθ = opposite/adjacent
- cosθ = adjacent/hypotenuse
- cscθ = 1/sinθ
- cotθ = 1/tanθ
- secθ = 1/cosθ
What is radian in Unit Circle?
In simple words, the radian in any shape is a way to measure different angles. In any shape, a radian gives you a specific angle that you need. The radian has a length that is equal to circle arc length. The orientation and size of the unit circle are not significant. However, for your information in a full circle, there are 2 radians with value 2π. Same as that, a half-unit circle equals the π radius value.
A brief explanation of the Unit chart:
The unit circle in trigonometry is famous as well as a common tool found in mathematics. It helps the users to know about the circle angles and the functions of trigonometry. All points are estimated beginning from the x-pivot in quadrant one and may circumvent the unit circle any number of degrees.
The circle points are in accordance with the terminal sides in each angle. They give the trigonometric capacity of the edge through their coordinates. The two central coordinates of the unit circle are cos and sin. Note that in trigonometry, a point can be of any size, positive or negative. The angle is not bigger than 360º because all the values are lie under 0 to 360º degree.
How can you make your own unit Circle Chart?
It requires a lot of practice and information to make a unit circle chart. Now follow the fantastic tips to make your own unit circle chart:
- Let’s start by making the first quadrant on a unit chart. Now create a 30-degree plot in the first quadrant for your unit circle.
- Now make a point and connect those points to the center point of the unit circle within a straight line.
- Likewise, ensure that the edge’s size is genuinely little. It should just be 33% of the path somewhere in the range of 0 and 90-degrees.
- Next, draw the opposite line. In doing this, you’ll have the option to make a right triangle.
- The hypotenuse of the triangle would fill in as the sweep of your unit circle. One the other ways sides of the angle placed on axis x while the other leg would be on the axis y.
- Discover the length by isolating the incentive by 2. For the longest side, you have to match the values by the shortest angle of the circle.
- You will get the option to make any name at the 30 degrees of your unit circle.
- You can use the bold and different alphabet to denote every angle and line.
- You can easily find out the length of your triangle sides. After this, you can identify the identities and functions in your unit circle.
- The second and fourth quadrants are just perfect representations of quadrant 1. The signs contrast in light of the fact that the focuses on the hover are in changing areas of the plane.