linear equation

Linear Equations Introduction

Introduction to Linear Equation

Linear equation is an equation that “plots a straight line on graphs”.

Standard form of Linear equation is:

Ax + By = C

 

Where A, B, C are the numbers (Coefficients) and x and y are the variables.

Example

            Ax + By = C

Just put numbers in above equation by replacing A, B and C.

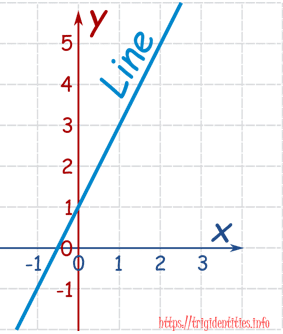
  1. Y = 2x + 1.
  2. 2x + 3y=7.
  3. 5x = 6 +3y.

If x increases, y increases double as fast.

Steps for solving linear equations

  1. Expands the brackets.
  2. Change the order of terms so that all variables are on L.H.S of equations and all constants are on R.H.S of equations.
  3. Combine like terms
  4. Solve like terms
  5. Find the solution and write the answer




Example

Linear equation graph for y = 2 x + 1.

 

linear equation

 

Example

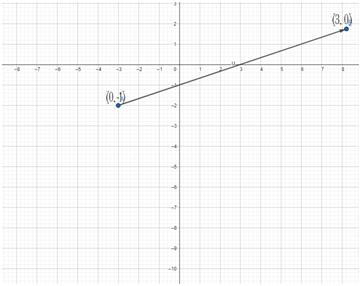
Draw a Graph of a linear equation x-3y=3.

Step1:

X- 3y = 3 //equation 1.

⇒For solving y we assume that x=0.

Putting x=0 in equation 1.

0 – 3y=3

⇒-3y=3

⇒Y = – 1

Step 2:

For solving x we assume that y=0

X – 3 (0) = 3

X = 3.

Step 3: draw a straight line between x=3 and y=-1

Graph between x and y (3, 0) and (0,-1)

Draw a straight line through it.

linear equation2

 

Example solving on linear equations:

Example 1:

(1x + 2) / (x + 3) = 1

(1x + 2) =1 (2x+ 3)

⇒1x + 2 = 2x + 3

⇒X – 2x = 3 – 2(Shifting X to L.H.S and constants to R.H.S)

We get

⇒-1x = 1       (Dividing both side by 3 we get)

⇒Answer X= -1.

 

Example 2:

3x – 10 = 6x – 19

3x – 10 = 6x – 19

⇒ 3x – 6x = – 19 + 10   (shifting 6x to L.H.S and -10 to R.H.S)

⇒ 3x = 9

⇒ 3x/3 = 9/3   (Dividing both sides by 3)

Answer x = 3

Example 3:

Solve the value of x

    5 (2x – 9) – 4x= 5 – 2x

⇒10x –45 – 4x = 5 – 2x

⇒10x -4x -2x =5 -45          (Shift all variables to L.H.S and all constants to R.H.S)

⇒4x = 40      (Dividing both side by 10)

Answer ⇒X= 10

Linear equation different form

There are many forms of linear equation but usually the equations have constant like 1, 2, 3…. & have simple variables like x-axis and y-axis.

Examples of non Linear equations

Linear functions have a constant slop while plotting on graphs it gives us straight line. While nonlinear functions have slop that varies between points.




⇒X2 – 4 = 0

⇒X2 /2 = 10

Linear Equation General Form

Ax + By + C = 0

Note:A and B can’t be zero at same time.

General form is not always useful.

Example

⇒4x + 2y + 4 = 0

Here

A = 4

B = 2

C = 4

Slop-intercept form

The equation slop intercept form is

Y=mx+b

Where“b” is the y-intercept and “m” is the slop of the points. Slop is always same if we change the order of operations.

Example 1

Y = -13 + 7x.

Step1

Y = -13 + 7x.

⇒For solving y value we Put x=0 we get

Y = – 13 + 7(0).

Y = – 13.

Step 2

For solving x we put y=0

⇒0= – 13 + 7x.

⇒13 = 7x(Dividing both side by 7)

X= 13/7

The slop interpret form of equation is (0, -13) and (13/7, 0).

 

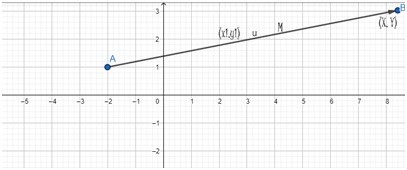
Point slop form

The equation of a straight line of “Point-slop” is

Y – Y1 =m(X – X1)

linear equation

Where X1 and Y 1 are given values and m is the slop of the line.

(X, y) are the unknown values.

Equations of point slop form

Where y1 and x1 is given m is slop of the equations and x and y is unknown values.

 

  • Y – 2 = 2(x-3)
  • y + 4= ½(x − 8)
  • y + 4= 4(x + 10)