The surface Area of a circle is quite different from all other shapes because of the round nature. However, there are many practical applications in everyday life where you need to calculate a circle area. The calculator for the circle area is not a complex one. All you need to know is the formula, and you can quickly understand the size of any circular object. Learn more about Trig identities on our website.
What is the area of a circle?
The area of a circle is any space that the circle occupies on a flat surface. When we talk about the surface area of the circle, we are focusing on two-dimensional objects. When finding the circle area, there are three other measures that we take into consideration, including the circumference, diameter, and radius. All three calculations also help us fining the circle area.
You can also learn about
Practical applications for circle area calculations
Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference. While most people think that formulas have no practical use, they are critical factors in many everyday life routines.
Architects use the symmetrical properties of a circle to design Ferris-wheels, buildings, athletic tracks, roundabouts, etc. These circular measurements are also significant for engineers in designing airplanes, bicycles, rockets, etc.
The circle is indispensable. In short, from designing a simple machine such as a clock to develop a complex nuclear reactor, circular calculations play a significant role.
How to find the area of a circle or what is the formula for finding the area of a circle
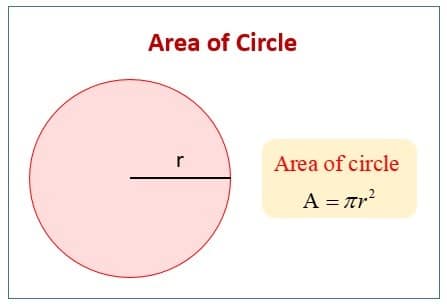
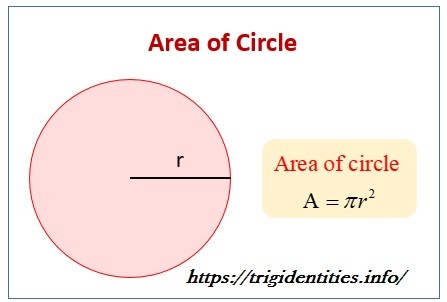
Many students have question in minds that what is the formula for finding the area of a circle? So answer is very simple the formula for the area of a circle is A = πr2. The number that is used to balance the equation of any circle is represented as π. It is a never-ending number that the Egyptians first discovered while calculating the area of a circle.
“R” is used to represent the radius of the circle. It is the distance of any line from the center of the circle to the circle’s edge. You can also calculate the radius by dividing the diameter by 2.
To remember the circle area formula, use the phrase ‘pie are squared, but they are round.”
Methods to derive the area of the circle:
Two methods prove the formula of the area of the circle, known as:
- Calculating circle area using rectangles
- Calculating circle area using triangles
Let’s take a look at these two methods to understand the area of the circle better.
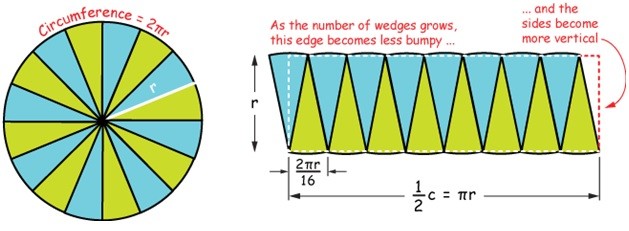
Calculating circle area using rectangles
In this method, we divide the circle into 16 equal sectors. The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors’ arc length would be equal. The circle’s area would be the same as the area of the parallelogram shape or rectangle.
Take a look at the above figure. In this image, you can see 16 sectors, including 8 green and 8 blue ones. The green highlighted sectors represent the circle’s half circumference while the other half of circumference is represented by blur highlighted ones. By increasing the number of the sectors cut from the circle, the parallelogram will change into a rectangle. The length of the rectangle would b equal to πr with a width equal to r.
It means that area of the circle is equal to the area of a rectangle. So, we have
A = πr×r (rectangle)
A = πr2 (circle)
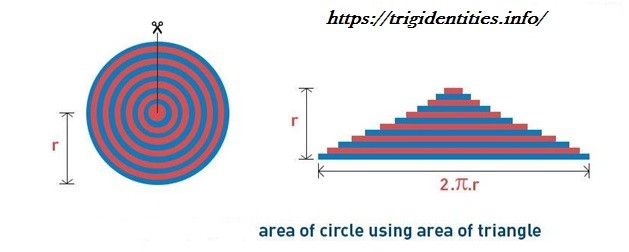
Calculating circle area using triangles
This method requires us to create concentric circles within a circle with radius r. When we cut the circle in a straight line from the center of the circle and spread the concentric circle lines, it will form a triangle. It is described in the image below
Now the height of a triangle is equal to the circle’s radius, while the triangle’s base is equal to its circumference. All of this indicates that both triangles and circles have equal areas. So the formulas would look something like this:
A = 1/2×base×height
A = 1/2×(2πr)×r
A = πr2
How to find the area of a circle with a radius?
If you are given the radius of a circle, then finding the area is quite simple. All you need to do is square the radius and multiply it with the Pi symbol. Although the value of π can be simplified to 3.14 for specific calculations, it is better to use the exact amount on a calculator.
Example
For example, if the radius of a circle is 6cm, then the squared radius would be 36cm. If you multiply this number by π, you will get a total surface area of 113.04cm squared. If you don’t have the value of π, you can represent the area by 36πcm squared.
A= πr2
A=113.04
How to find the circumference of a circle?
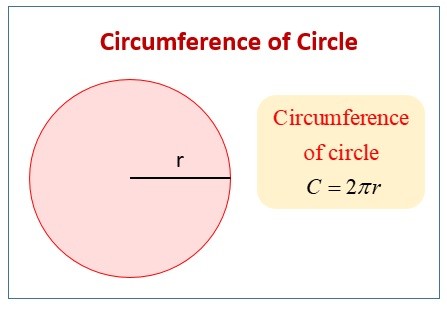
The circle circumference is the perimeter of an elliptical or circular shape. In other words, this is the arc length or boundary length of the circle; if we straightened it out or open up in a line segment.
To understand it better, take a look at the figure below:
There is a piece of rope and a circle. The o is the center point of the circle, and r is the radius. Now the circle’s circumference or perimeter would be precisely the rope’s length that wraps around the circle.
In the above figure, you can see two formulas. C represents the circle’s circumference in the first formula, also denoted as P.
How to find the area of a circle with diameter?
Finding the radius is not always easy, especially if you don’t have the circle’s center. You can calculate the area using the diameter instead. The same formula applies as above, but you need first to calculate the radius of the circle. Simply divide the diameter by 2 to get the radius.
Example
For example, if the diameter is 12cm, then the radius will be 6 cm. Once you have the radius, you can use the same formula as mentioned above.
This formula applies to any circle to get the surface area. Also, remember that the value of π will be the same, regardless of the circle size.
Explaining the circle formula with a “Real World” example
Now that we have known all the formula of a circle and the three significant elements – diameter, radius, and circumference – let’s apply these formulas using a real-life example. So we can understand the formulas and their importance more clearly:
Example: Mr. Smith is constructing a house for Brandon. To build the house, he needs to create the base first; he needs to drill some holes and fill in the concrete. But do you think that he can drill any size of the holes? No! All the holes must be 0.5m wide and 1.5m deep. So how much concrete should Mr. Smith order to fill all the holes?
Here is how he can know:
As the holes are 0.5 m wide and circular, the diameter of the circle would be 0.5m. So the Area of the circle would be calculated as:
A=1/4πD2
A= ¼*π*(0.5)2
A=0.785m2
Now the depth of the holes is 1.5m. So using this, we can easily calculate each hole’s volume using the volume formula area x depth.
Volume = Area of the circle x depth
Volume = 0.785*1.5
Volume = 1.177 m3