Inverse Trig Identities Trig Double Identities Trig Half-Angle Identities Pythagorean Trig Identities
Trig Identities – Trigonometry is an imperative part of mathematics which manages connections or relationship between the lengths and angles of triangles. It is a significant old idea and was first utilized in the third century BC. This part of science is connected with planar right-triangles (or the right-triangles in a two-dimensional plane with one angle equivalent to 90 degrees).
Students are educated about trigonometric identities or properties in school and it a critical piece of a more elevated amount of science. So, to enable you to comprehend and become familiar with every single trig character we have clarified here every one of the ideas of trigonometry.
As a student, you would locate the trig Identities Worksheet we have given here valuable. So, you can download and print the trig identities PDF and use it whenever to solve the questions related to trigonometric.
Despite the fact that trigonometry does not have any immediate application its application in our everyday lives can’t be disregarded. It is a vital part of numerous zones of studies and ventures. Its most regular application is to gauge the stature of a building, mountain, or a tall article at a separation. The main two data required to discover the tallness is the point of rising and separation from the article.
PRACTICAL IMPLICATION OF TRIGONOMETRY
There are some different branches where trigonometry has contributed monstrously in its development and advancement. A portion of its fields of use are mentioned below
In music: It can be utilized to create music carefully, through PC.
In-Aviation: It is of imperative significance to lead an airplane in the right direction. For example, if the airspeed and the angle of the jets are known, it very well may be utilized to decide the heading of the aircraft.
In criminology – Trigonometry can likewise be utilized in criminology where it is utilized to ascertain different essential determinants of a wrongdoing scene, for example, the direction of a shot, how a victim object falls, and so forth.
Mathematics or Arithmetic Calculations: Trigonometry is a standout amongst the most essential parts of science, without which some other imperative branches couldn’t have existed. For instance, analytics is absolutely founded on trigonometry and polynomial math.
WHAT ARE TRIG IDENTITIES?
Trig identities or Trigonometric identities are actually the mathematics equations which are comprised of trigonometric functions. And these trig identities are valid for any estimation of the variable put.
There are numerous trigonometric identities which are determined by the essential trigonometric functions for instance sin, cos, tan, and so forth. The most fundamental trigonometric function is the Pythagorean Trigonometric Identities, which is gotten from the Pythagoras Theorem. It is utilized to decide the trigonometric function or values by applying the Pythagoras Theorem. So, it encourages us to decide the connection among lines and angles in a right-calculated triangle.
The other vital trigonometric characters are Hyperbolic trig identities, half-point trig characters, opposite trig characters, and so forth. You can easily explore multiple trig identities on this website.
In math’s world, trigonometry is the mixture if geometry and calculations. While studying the trigonometry branch, you must find the connection between the sides of the triangles and their angles. Did you ever notice the ‘tri’ in a triangle as well as in the branch trigonometry? Try not to mix up both terms.
Trigonometry isn’t just about triangles! Numerous shapes can be broken into different triangles, so your insight into trigonometry can assist you with numerous different shapes. Trigonometry utilizes equations to help you with making the idea of unknown estimations of the edges and angles of triangles in trigonometry.
LIST OF TRIGONOMETRIC FORMULAS BRIEF EXPLANATION
Trigonometry is an essential branch of mathematics that occupy with all sort if triangles and their measurements. The branch also describes the secure connection between the angle and length of the triangles. There are a tremendous number of uses of trigonometry and its formulas. For instance, the procedure of triangulation is utilized in Geography to quantify the separation between tourist spots; in Astronomy, to measure the distance between starts and used in satellite routing systems.
TRIGONOMETRY FORMULAS LIST
When we start learning about the trigonometric formulas, we first have to consider the right angle triangle. It allows us to understand the equations and their functions efficiently. Well, we all know that in the triangle, we have three sides in particular. The three sides of the right angle triangle are Hypotenuse, Adjacent side (Height), and Opposite side (Perpendicular). The longest side of the triangle is known as the hypotenuse, and the side inverse to the point is called perpendicular. The side where both hypotenuse and perpendicular are resting together is known as the adjacent side.
HERE IS THE RUNDOWN OF EQUATIONS FOR TRIGONOMETRY
There are fundamentally six trigonometry ratios utilized for finding the components in Trigonometry. They are called trigonometric ratios or functions. The six trigonometric ratios are sine, cosine, secant, and their reciprocals are cosecant, tangent, and cotangent, respectively. If we use the right angle triangle as a kind of perspective, then, the trigonometric ratios derived as:
- sin θ = Opposite Side/Hypotenuse
- cos θ = Adjacent Side/Hypotenuse
- sec θ = Hypotenuse/Adjacent Side
- tan θ = Opposite Side/Adjacent Side
- cosec θ = Hypotenuse/Opposite Side
- cot θ = Adjacent Side/Opposite Side
TRIGONOMETRY RECIPROCAL IDENTITIES:
The Reciprocal Identities of the right angle triangle are given as:
- cosec θ = 1/sin θ
- cot θ = 1/tan θ
- sec θ = 1/cos θ
- cos θ = 1/sec θ
- sin θ = 1/cosec θ
- tan θ = 1/cot θ

GET TO KNOW ABOUT TRIGONOMETRY TABLE
Based on the right-angle triangle, we will further share each trigonometry ratio’s values at different angles.
| Angles (In degree) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Csc | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| Sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
UNDERSTANDING THE MAJOR SYSTEM OF TRIGONOMETRY FORMULAS
Do you know that all six trigonometric formulas are further divided into major systems known as Trigonometric Identities and Trigonometric Ratios? Well, these two major systems show the different concepts of these formulas. Also, we will check how they both are different from each other.
The tri identities are valid for all triangle estimated factors. The Trigonometric Ratio speaks about the connection between the estimation of the edges and the length of the side of the right-angle triangle.
The six tri formulas are useful for the understudies in taking care of issues dependent on these equations or any trigonometric application. Alongside these, trigonometric functions help us to determine the trigonometric formulas, which are found out in the assessment. We additionally give the essential trigonometric formulas table that offers the connection of every single trigonometric capacity alongside their standard worth. These trigonometric formulae are useful in deciding the area, range, and estimation of each trigonometric function.
CONCEPT AND CONNECTION OF SHIFTS AND PERIODICITY:
By shifting the claims of further trigonometric ratios using specific points, changing the signs, or using correlative trigonometric functions will allow you to express specific outcomes at any level. We have mentioned some examples of shifts in the below table.
- A full turn or period is also known as 360° or 2π radian. It may allow the unit circle to get the fixed ratio and the limited time for which the three main trigonometric ratios repeat their qualities in a specific period.
- A half-turn or half period is also known as 180° or π radian. It is the time of tan(x) = sin(x)/cos(x) and can be seen from these trigonometric capacities.
- With full period 2π, a large portion of ratios changes the indication of their qualities. Altogether, they change the sign by any odd numerous of π with k a subjective whole number. Any even various of π is obviously only a full period, and a regressive move significantly a period is equivalent to a retrogressive move by one full period in addition to one move forward considerably a period.
| The shift of one quarter period | The shift of one half period | The shift of the full period | Period |
| Sin | cosθ | -sinθ | sinθ |
| Cos | -sinθ | -cosθ | cosθ |
| Tan | -cotθ | tanθ | tanθ |
| Csc | secθ | -cscθ | cscθ |
| sec | -cscθ | -secθ | secθ |
| cot | -tanθ | cotθ | cotθ |
A quarter turn, or 90°, or π/2 radian is a half-period move for tan(x) and cot(x) with period π (180°), yielding the capacity benefit of applying the corresponding capacity to the un-shifted contention. With the contention to their quarter’s values, you can select any odd number with equation (2k + 1) π/2 in the half time frame.
With all trigonometric functions, a circle first quarter likewise moves to a full or half quarter period. A move by a quarter period isn’t secured by a half period. It can be disintegrated in a number of periods, give or take a one-quarter period. The terms of communicating these products are (4k ± 1) π/2.
The reverse movements by one-quarter period are reflected in the table beneath. Once more, these movements yield work esteems, utilizing the particular reciprocal capacity applied to the un-shifted contention. Moving the contentions of tan(x) and cot(x) by their quarter period (π/4) doesn’t yield such basic outcomes.
MORE ABOUT ORIGIN OF TRIGNOMETRY
Let’s assume that you are making a treehouse. You place a large ladder against the tree trunk at the top side. You must feel that it is too tall for you to climb the tree. So you need first to calculate the tree trunk height to evaluate that. So is there any appropriate way to measure the tree trunk height?
If you already know the angle of the ladder and judge how far the trunk is placed, you can figure out the exact height of the truck with the help of trigonometry. You may get the fundamental importance of trigonometry with this example. Further, we will move to the actual meaning of this mathematics branch.
HISTORY OF TRIGONOMETRY
Did you realize that trigonometry began as an approach to examining planets and stars? Quite a while prior, individuals believed that the planets and stars rotated around the Earth. We know the specific inverse is valid. Stars have a fixed situation in the sky, and the Earth and different planets rotate around the Sun.
To contemplate this development, a space expert named Hipparchus understood that you could interface the Earth with different planets or stars with the nonexistent right (triangles with a point formed like a corner). What’s more, trigonometry was conceived! Hipparchus is known as the grandfather of math’s branch Trigonometry.
TRIGONOMETRY APPLICATIONS
- Their application is in different fields like oceanography, seismology, meteorology, physical sciences, stargazing, acoustics, route, hardware, etc.
- It is additionally useful to gauge the stature of the mountain, discover the separation of long streams, and so forth.
- The term and its functions are a bit popular in astronomy and satellite applications.
- It plays a huge role in medical sectors and engineering.
UNDERSTANDING TRIGONOMETRY VOCABULARY
One of the most important things to know about trigonometry is its vocabulary and important functions. Although it has three main functions, you will explore a great set of vocabulary. It is a kind of secret code, and before going to use, then you need to know about their names and meanings. Trigonometry is the most extensive branch that uses a great set of words that describe triangle parts differently. Some of the important vocabulary and their functions are:
-
RIGHT ANGLE TRIANGLE:
It is a part of a triangle that has a right angle with a straight line. The angel with a straight line is denoted by 90 degrees. The interesting fact is that a triangle has only one right angle. The standard trigonometric proportions must be utilized on a 90-degree angle of all triangles.
-
HYPOTENUSE:
The longest side of the triangle is known as hypotenuse. It is the side that is opposite to the right angle. For instance, for the triangle on the right, the hypotenuse is side c.
-
THE OPPOSITE OF AN EDGE:
The contrary side of an edge is the side that doesn’t meet with the vertex of the edge. For instance, the side is something contrary to angle A in the triangle to one side.
-
EDGE ADJACENT:
It is the side that crosses the vertex of the edge yet isn’t the hypotenuse. For instance, side b is adjoining angle A in the triangle to one side.
CONCEPT OF TRIGONOMETRY RATIOS
There are three main ratios of trigonometry Sine, Cosine, and tangent. The trigonometric proportions of a triangle are also known functions of trigonometry. Let us perceive how are these proportions or capacities, assessed on account of a 90 degree. Further, we will check what the functions and reciprocals of these three main ratios are.
These are six important trigonometric functions that have different abbreviations and relationships with the right angle of the triangle.
| Functions name | Their abbreviations | Relationship with their right-angle triangle |
| Sine | Sin | Opposite side / Hypotenuse |
| Cosine | Cos | Adjacent side / Hypotenuse |
| Tangent | Tan | Opposite side / Adjacent side |
| Cosecant | Cosec | Hypotenuse / Opposite side |
| Secant | Sec | Hypotenuse / Adjacent side |
| Cotangent | cot | Adjacent side / Opposite side |
A DETAILED GUIDE ON ALL TRIGONOMETRY ANGLES
The three essential angles in trigonometry are sine, tangent, and cosine. In view of these three functions, the other three capacities that are cotangent, secant, and cosecant are determined. All the trigonometrically ideas depend on these three formulas. Subsequently, to comprehend trigonometry further, we have to learn first these three functions and their individual formulas.
Let’s suppose that θ is the edge in a right-angle triangle, at that point.
- Sin θ = Perpendicular/Hypotenuse
- Tan θ = Perpendicular/Base
- Cos θ = Base/Hypotenuse
- The opposite is the side inverse to the point θ of the right angle.
- The base is the contiguous side to the angle edge θ.
- The hypotenuse is the side inverse to the right point of the angle.
The trigonometry points which are generally utilized in trigonometry issues are 0°, 30°, 45°, 60°, and 90°. The trigonometric proportions, for example, sine, cosine, and digression of these points, are anything but difficult to remember. We will likewise show the table where all the proportions and their separate point’s qualities are referenced.
To discover these edges, we need to draw a right-calculated triangle, in which one of the intense points will be the relating trigonometry edge. These edges will be characterized as the proportion related to it. For instance, in a right-angle triangle:
- Sin θ = Perpendicular/Hypotenuse or on the other hand θ = sin-1 (Perpendicular/Hypotenuse)
- Likewise,
- θ = tan-1 (Perpendicular/Base)
- θ = cos-1 (Base/Hypotenuse)
UNIT CIRCLE & TRIG IDENTITIES – RELATIONSHIP BETWEEN UNIT CIRCLE & TRIGONOMETRY
UNIT CIRCLE & TRIG IDENTITIES
In science, the identities of trigonometric are those equalities that include all the primary functions. The identities are valid for all factors where the two sides of the equality are characterized. Geometrically, these are the significant identities, including some aspects of at least one edge. They are depended on the triangle identities, which are characters conceivably including edges yet additionally including side lengths or different lengths of a triangle.
These trigonometry identities are helpful at whatever point when the expression involves all functions which need to be simplified. A significant application is the incorporation of non-trigonometric functions. It is a typical procedure that includes first utilizing the preferred rule. After that, the substitution rule applied to all functions simplifies the results that are subsequent vital with all trigonometric identities.
Lets simply this in mathematics the word “Identity” is a condition that is in every case remain true. These can be “inconsequentially” true, similar to “x = x”. For example, the Pythagorean Theorem’s “a2 + b2 = c2” always remains true for right triangles. There are heaps of trigonometric identities present; however, coming up next are the ones you’re destined to see and use in all ways.
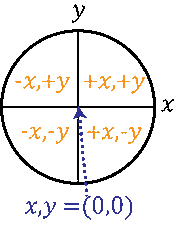
UNDERSTAND THE TRIGONOMETRY CONCEPT IN CIRCLE:
For all diameter circles and curved shapes, the trigonometry identities will remain the same. Not only at right-angle triangles, but the trigonometric functions are also applicable on all sorts of angles range from 0 to 360°. If you want to understand the functions that work in all angle quadrants, it is perfect to think about the triangles in a circle and their values.
Let’s consider the Circle what is divided into four quadrants with equal diameter. The center point of Circle is regarded as a Cartesian arrangement of (0, 0). At the center point, the value of X is 0. Same as that, the value of Y,= is also 0. These values remain constant on the origin point.
Thus any place under the beneath of the middle point has a y value that is estimated under 0 or may go in negative counts.
FUNDAMENTAL AND PYTHAGOREAN IDENTITIES
Trig proportion is consistently complementary of some “non-co” proportion. You can use these functions and identities that will allow you to keep level records. To evaluate the axis values, cosecant goes with the sine, and the secant goes with the cosine values. Following, we state the Pythagorean Identities.
- Sin2 (t) + cos2 (t) = 1
- 1 + cot2 (t) = csc2 (t)
- tan2 (t) + 1 = sec2 (t)
Note that the three Pythagorean Identities most importantly include figuring out and the number 1. First you have to see the Pythagorean Theorem for th understaidn of their relationship. The edge is t, the “inverse” side is sin (t) = y, the “nearby” side is cos (t) = x, and the hypotenuse is 1.
We have extra characters identified with the status of the trigonometry ratios:
- Sin (– t) = – sin (t)
- Tan (– t) = – tan (t)
- cos(– t) = cos(t)
Notice specifically that tangent and sin are two popular functions of trigonometry. You need to be symmetric about the circle origin, while cosine is a function.
WHAT ABOUT THE DOUBLE-ANGLE AND HALF-ANGLE IDENTITIES
| Double angle identities |
| sin(2x) = 2 sin(x) cos(x) |
| cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1 |
HALF ANGLE IDENTITIES
With the use of trigonometry functions and identities, you can derive the half-angle identities easily. To conclude this, you have to first prove the identities. Proving the identities of trigonometry alludes to indicating that the personality is in every case valid, regardless of what sort of value of theta (θ) is utilized.
The value needs to remain constant for all estimations of xx. We can’t just substitute in a couple of xx estimations to “show” that they are equivalent. It is conceivable that the two sides are equal to a few qualities, and we may feel that we have an identity with true value.
Rather, we need to utilize sensible strides to show that one side of the tri equation can be changed to the opposite side of the trigonometry equation. Now and again, we will work independently on each side of the triangle.
GENERAL APPROACH TO PROVE THE TRIGONOMETRY IDENTITIES
To prove the identities, you need to first familiar with all trigonometric identities. You have to first remember the Pythagorean identities and all related tri functions. There is a wide range of approaches to demonstrate each identity easily. Here are a few suggestions that you need to follow to prove all trigonometry identities:
- Keep the focus on the sides of the triangle that are complicated to resolve. Try to simplify the identity and rearrange it.
- Replace every single trigonometric operation with the use of sin and cos functions where needed.
- Identify all simple algebraic operations like considering, growing, distributive property, and fractions. It will allow you to simplify the trigonometry identity.
- You can use the different trigonometric identities and keep an eye out for the Pythagorean functions.
- Keep an eye on the opposite side of the equations, and work towards it.
- Now consider the “trigonometric conjugate” to prove it.
Trigonometry identities are supposed to be the most significant and important scientific relationship at any point.
The point when we start to consider the applications where exact separations are significant, it is obvious that there are handfuls, route for maritime and flying frameworks, space science, satellite frameworks, geological overviews and maps, basic building, visual computerization and different Technology generated applications found utilizes their identities and expressions.