Inverse Trig Identities

The inverse trigonometric identities or functions are additionally known as arcus functions or identities. Fundamentally, they are the trig reciprocal identities of following trigonometric functions

  1. Sin
  2. Cos
  3. Tan

These trig identities are utilized in circumstances when the area of the domain area should be limited.

These trigonometry functions have extraordinary noteworthiness in

  • Engineering.
  • Air & Road Navigations.
  • Physics.
  • Geometry.
  • Many others

Here we have offered you with the table appearing Inverse trigonometric identities or functions of all the basic trigonometric identities

inverse trig identities

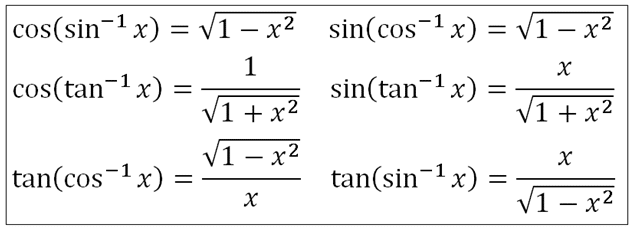
Properties of Inverse Trig Identities

Property 1

  1. sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1
  2. cos-1 (1/x) = sec-1x , x ≥ 1 or x ≤ -1
  3. tan-1 (1/x) = cot-1x , x > 0

Proof : sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1,

Let  sin−1x=y
i.e. x = cosec y
1x=siny
sin−11x)=y
sin−11x)=cosec−1x
sin−1(1x)=cosec−1x
Hence, sin−11x=cosec−1x where, x ≥ 1 or x ≤ -1.

Property 2

  1. sin-1(-x) = – sin-1(x),    x ∈ [-1,1]
  2. tan-1(-x) = -tan-1(x),   x ∈ R
  3. cosec-1(-x) = -cosec-1(x), |x| ≥ 1

Proof: sin-1(-x) = -sin-1(x),    x ∈ [-1,1]
Let,  sin−1(−x)=y
Then −x=siny
x=−siny
x=sin(−y)
sin−1=sin−1(sin(−y))
sin−1x=y
sin−1x=−sin−1(−x)
Hence,sin−1(−x)=−sin−1 x ∈ [-1,1]

Property 3

  1. cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
  2. sec-1(-x) = π – sec-1x, |x| ≥ 1
  3. cot-1(-x) = π – cot-1x, x ∈ R

Proof : cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
Let cos−1(−x)=y
cosy=−x   x=−cosy
x=cos(π−y)
Since,  cosπ−q=−cosq
cos−1x=π−y
cos−1x=π–cos−1–x
Hence, cos−1−x=π–cos−1x

Property 4

  1. sin-1x + cos-1x = π/2, x ∈ [-1,1]
  2. tan-1x + cot-1x = π/2, x ∈ R
  3. cosec-1x + sec-1x = π/2, |x| ≥ 1

Proof : sin-1x + cos-1x = π/2, x ∈ [-1,1]
Let sin−1x=y or x=siny=cos(π2−y)
cos−1x=cos−1(cos(π2−y))
cos−1x=π2−y
cos−1x=π2−sin−1x
sin−1+cos−1x=π2
Hence, sin-1x + cos-1x = π/2, x ∈ [-1,1]

Property 5

  1. tan-1x + tan-1y = tan-1((x+y)/(1-xy)), xy < 1.
  2. tan-1x – tan-1y = tan-1((x-y)/(1+xy)), xy > -1.

Proof : tan-1x + tan-1y = tan-1((x+y)/(1-xy)), xy < 1.
Let tan−1x=A
And tan−1y=B
Then, tanA=x
tanB=y
Now, tan(A+B)=(tanA+tanB)/(1−tanAtanB)
tan(A+B)=x+y1−xy
tan−1(x+y1−xy)=A+B
Hence, tan−1(x+y1−xy)=tan−1x+tan−1y

Property 6

  1. 2tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1
  2. 2tan-1x = cos-1((1-x2)/(1+x2)), x ≥ 0
  3. 2tan-1x = tan-1(2x/(1 – x2)), -1 < x <1

Proof : 2tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1
Let tan−1x=y and  x=tany
Consider RHS. sin−1(2×1+x2)
=sin−1(2tany1+tan2y)
=sin−1(sin2y)
Since, sin2θ=2tanθ/(1+tan2θ),
=2y
=2tan−1x which is our LHS
Hence 2 tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1

Solved Example

Q1. Prove that “sin-1(-x) = – sin-1(x),    x ∈ [-1,1]”

Ans: Let, sin−1(−x)=y
Then −x=siny
x=−siny
x=sin(−y)
sin−1x=arcsin(sin(−y))
sin−1x=y
sin−1x=−sin−1(−x)
Hence, sin−1(−x)=−sin−1x, x ∈ [-1,1]

This concludes our discussion on the topic of trigonometric inverse functions.