Today we are going to discuss one more basic term of mathematics Sine Cosine and Tangent . In short these terms are also call sin cos and tan .
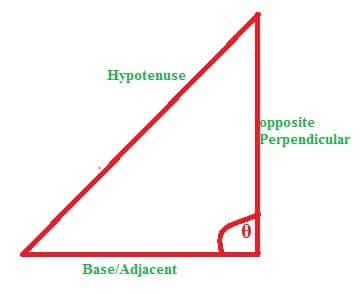
Sine, Cosine and tangents are the important terms in trigonometry and their definition based on Right angle triangle. Basically they are defined in terms of ratio to the sides of right angle triangle. Right angle triangle is type of triangle in which one angle is 90.
Before start to discuss about the main topic sin cos and tang we have to touch the basic of Right angle triangle.
In right angle triangle hypotenuse is the longest side opposite to the right angle. and perpendicular is the side of angle 90 .
Sine Cosine and Tangent
So according to figure we can easily discuss about sine, cosine and tangent (sin, cos, tan).In any right angled triangle
Sine θ = The length of the perpendicular
The length of the hypotenuse
Cos θ = The length of the Base
the length of the hypotenuse
Tan θ = The length of the perpendicular
The length of the Base
Easy way to learn sin cos tan formulas
We will discuss two methods to learn sin cos and tang formulas easily. Students need to remember two words and they can solve all the problems about sine cosine and tangent.
Method 1
You can learn easily formula of sin cos and tan by learning word SOHCAHTOA.So now we disucss how it works to remember the formula
|
Abbreviations |
Formulas |
|
SOH |
Sin θ=Opposite/Hypotenuse |
|
CAH |
Cos θ=Adjacent/Hypotenuse |
|
TOA |
Tan θ=Opposite/Adjacent |
In short if we took above abbreviations we can easily remember the sine formula by remembering SOH. Same way we can learn Cosine formula by remembering CAH and tangent formula with TOA.
Method 2
In above method we discuss to learn formulas for sin cosine and tangent by remembering single word. In same way this is second method to learn these formulas easily. According to right triangle if you learn these 3 sentences you can easily learn the formulas for sin cos and tan.
|
Sentences |
Formulas |
| Some People have |
Sin θ=Perpendicular/Hypotenuse |
| Curly black hair |
Cos θ=Base/ Hypotenuse |
| Through proper brush |
Tan θ= Perpendicular /Base |
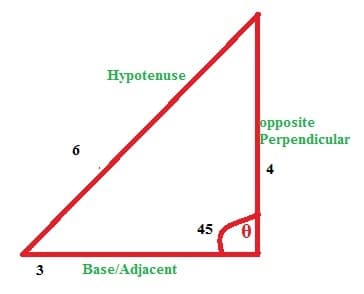
Example: What is the sine cos and tang of 45°?if Perpendicular is 4 ,Base is 3 and hypotenuse is 6.
From figure we have value of θ= 45.
Hypotenuse = H= 6
Base = B= 3
Perpendicular = P= 4
By using sine formula
Sin (θ) = Perp/Hyp
Sin (45) = 4/6 Sin (45) = 0.666
By using cosine formula
Cos (θ) = Base/Hyp
Cos (45) = 3/6 Sin (45) = 0.5
By using tan formula
Tan (θ) = Perp/Base
Tan (45) = 4/3 Tan (45) = 1.33
Learn more about trig identities & Unit circle