Introduction to Trigonometry
What is trigonometry?
The word trigonometry arises from three Greek words. Tri meaning three, gono meaning angle and metry meaning measurement. Thus, trigonometry is a branch of Mathematics which deals with sides, angles and functions related to sides and angles of a triangle.As we already discussed about Trig Identities Today we are going to discuss about Trigonometric ratios and Trigonometric Functions .
The main contributors to this branch of Mathematics are Muhmmad Bin Musa Alkhawarzimi, Abu-Abdullah Albatafi and Alberuni.
Trigonometric Ratios
A trigonometric ratio is a ratio of lengths of two sides in a right-angled triangle (A right angle triangle is a triangle that has on angle equal to 900). These ratios are used to find the measure of a side or an acute angle (which is less than 900) in a right-angled triangle.
Definition of Trigonometric Ratios
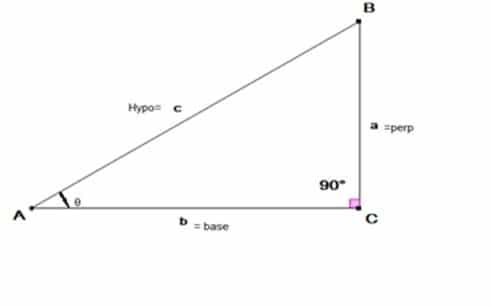
The trigonometric ratios for any acute angle θ of a right-angled triangle ABC are defined as:
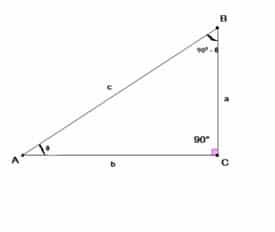
Suppose we have a right-angled triangle ABC. Such that m ∠ BAC = θ and m ∠ ACB =900 as shown in figure 1 below
Figure 1:
Here the side opposite to the given angle θ is perpendicular. The side opposite to 900 angle is hypotenuse (A hypotenuse is always the longest side of a right-angled triangle) and the side adjacent to the given angle θ is called base. Thus, from the given information above we can define the trigonometric ratios of the given angle θ as given in the Table 1 (their reciprocal ratios are also given in front of them) .
| Table 1: The formula of Trigonometric Ratios and their Reciprocal Ratios | |
| Sin θ = Perp/Hypo =a/c | Cosec θ =Hypo/Perp = c/a |
| Cos θ = Base/ Hypo = b/c | Sec θ = Hypo/Base = c/b |
| Tan θ = Perp/base =a/b | Cot θ = Base/Perp =a/b |
There is also an easy trick to remember these ratios. The students first need to learn the following sentence by heart “Some People Have Curly Brown Hair To Proper Brush”. Now focus on the first letter of every word in the given sentence. It gives the formula of the first three trigonometric ratios given in Table 1. For convenience and simplicity purpose we have used bold faced and underlined the first alphabets of every word.
Trigonometric Ratios with the help of Unit Circle:
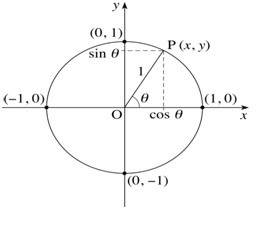
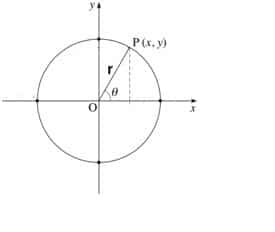
Trigonometric ratios can also be calculated by using a unit circle (A circle with radius 1 unit). Here we clear the concept of trigonometric ratios via unit circle.
Suppose we have a unit circle with center at O. Take a point P (x , y) anywhere on the circle. Join OP (which is the radius of the circle). The radius OP makes an angle θ with the x-axis. By drawing a perpendicular from point P (x , y) on x-axis we get a right-angled triangle in which m ∠ A = 900. By applying previous discussion on figure 2. We get the trigonometric ratios of a right-angled triangle via unit circle.
Figure 2:
| Table 2: The formula of Trigonometric Ratios and their Reciprocal Ratios Via Unit Circle | |
| Sin θ =Perp/Hypo =y | Cosec θ = Hypo/Perp = 1/y |
| Cos θ =Base/ Hypo = x | Sec θ = Hypo/Base = 1/x |
| Tan θ = Perp/base =y/x | Cot θ = Base/Perp =x/y |
Trigonometric Ratios of an Acute angle:
Here we explain how to calculate the trigonometric ratios of an acute angle in a right-angled triangle.
- Trigonometric ratios of 450
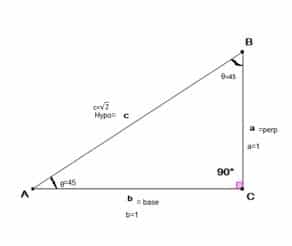
Consider a right-angled triangle with m ∠ c = 900 and m ∠ A = m ∠ B = 450 in figure 3. Note that because we have 450 angles on both A and B vertices therefore for both the vertices opposite side is perpendicular and its value must be same i.e. a=b=1 as can be seen from figure 3. Then to calculate the value of the third side we use Pythagoras theorem a2+b2=c2. The value of c becomes /√2 . Thus, following trigonometric ratios formula from Table 1 we have
| Table 3: The formula of Trigonometric Ratios 450 | |
| Sin 45 =Perp/Hypo=a/c= 1/√2 | Cosec 45 = Hypo/Perp = c/a = √2 |
| Cos 45 =Base/ Hypo = b/c= 1/√2 | Sec 45 = Hypo/Base = c/b= √2 |
| Tan 45 =Perp/base = a/b =1 | Cot 45 = Base/Perp = a/b = 1 |
Figure 3:
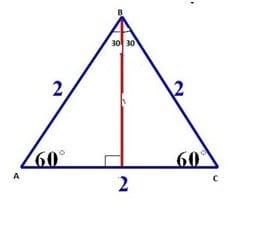
- Trigonometric ratios of 300 and 600
Consider an equilateral triangle (A triangle whose all sides and angles are equal) of side 2 units. Such that m AC = 2 units, so m AD = m DC = 1 unit. By applying Pythagoras theorem we have m BD =√3 units. Then from figure 4 we have the values of perp = 1 unit, hypo = 2 units and base =√3 for 300 angle. And pere = √3 , hypo = 2 and base = 1 for 600 angle. Thus from using the formula given in Table 1, we get the values of trigonometric ratios for 300 and 600 acute angles, which are given in table 4 and table 5 respectively
Figure 4
| Table 4: The formulae of Trigonometric Ratios 300 | |
| Sin30=Perp/Hypo=a/c=1/2 | Cosec30=Hypo/Perp=c/a=2 |
| Cos30=Base/Hypo=b/c=√3/2 | Sec30=Hypo/Base=c/b = 2/√3 |
| Tan30=Perp/Base=a/b=1/√3 | Cot30=Base/Perp=a/b=√3 |
| Table 5: The formulae of Trigonometric Ratios 600 | |
| Sin60=Perp/Hypo=a/c=√(3/2) | Cosec60=Hypo/Perp=c/a=2/√3 |
| Cos60=Base/Hypo=b/c=1/2 | Sec60=Hypo/Base=c/b = 2 |
| Tan60=Perp/Base=a/b=√3 | Cot60=Base/Perp=a/b=1/√3 |
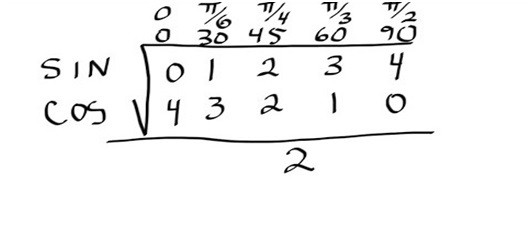
In the next table 6 we will provide trigonometric ratios for 00, 300, 450, 600 and 900 angles and a very simple trick to remember these values.
| Table 6 | |||||
| Ratio | 00 | 300 | 450 | 600 | 900 |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
It is worth mentioning here that Tan θ =sinθ/cosθ , so the students do not need to remember or learn the values of the remaining trigonometric identities as all of them can be calculated from the two basic ratios i.e. from Sin and Cos.
TRICK to Memorize the Values of Trigonometric Ratios Easily:
Write the angles in degree/radian measures in a row as can be seen in the below picture on the right-hand side of the angles write Sin in the first row and Cos in the second row and take square root after these ratios. Write the numbers from 0 to 4 for sin and 4 to 0 for cos values. After doing this, whatever value you need just divide the number after taking square root by 2. Below picture illustrates the method.
Solution of Right-Angled Triangle Using Trigonometric Ratios:
In this section with the help of a few examples we’ll try to clear the concepts of trigonometry.
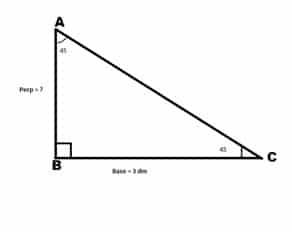
Example 1: In a right angled-triangle the base is 450 whereas the base length is 3dm. Find the length of perpendicular?
Solution: From the given data in the problem we have the figure.
Because we have base given and perpendicular is need. Therefore, we’ll use Tan θ to compute the result.
We know that Tan θ =Perp/Base
Putting values from above figure we get
Tan 45 =Perp/3 (using Tan 45 = 1)
1 = ⇒ Perp = 3 dm
Real Life Problems on Trigonometry:
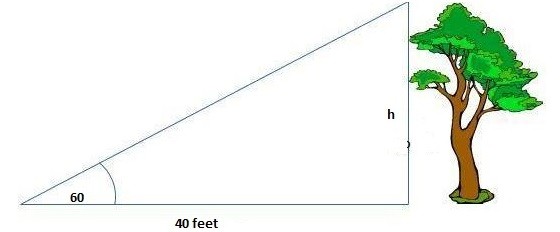
Example 2: In the given figure how tall is the tree?
Solution: The height of the tree is denoted by h. Because we are given base length and we need to find the height (which is the perpendicular) therefore we will apply Tan θ
We know that Tan θ =Perp/Base
Putting values from above figure we get
Tan 60 = h/40 (using Tan 60 =√3 )
√3 = h/40 ⇒ h = 40 x√3 ⇒ h = 69.3
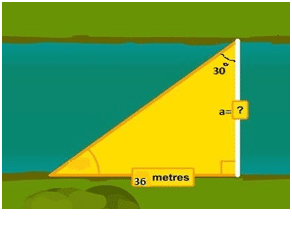
Example 3: Find the “a” distance across the river?
Solution: From the above figure we have given angle θ = 300, Perpendicular = 36 meters and base =? (Which is the required distance a). Therefore, we apply Tan θ here:
We know that Tan θ = Perp/Base
Putting values from above figure we get
Tan 30 = 36/a (using Tan 30 = 1/√3 )
1/√3 =36/a ⇒ a = 36 x√3
⇒ a = 62.3538 m
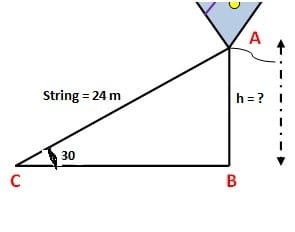
Example 4: A little boy is flying a kite. The string of kite makes an angle of 300 with the ground. Find the height of the kite when string is 24 meters long?
Solution: The below figure illustrates the examples
Here we have hypo = 24 m and given angle θ = 300 and perp =? (Which represents the height of the kite in meters). Therefore, we’ll use Sin θ
We know that Sin θ =Perp/Hyp
Putting values from the above figure, we get
Sin 30 =h/24 (using Sin 30 = 1/2)
1/2 =h/24 ⇒ h =24/2
⇒ h = 12 meters
Trigonometric Ratios of Complementary Angles:
When the sum of two angles is 900 the angles are said to be complementary angles. Here we explain how to obtain trigonometric ratios of complementary angles. Consider a right-angled triangle ABC such that m ∠ c = 900 and m ∠ A = θ therefore m ∠ B = 900 – θ. See the figure 5 for visualization of the problem.
Figure 5:
Keeping in mind previous discussion and applying the ratios formula from Table 1, we get
Sin (900 – θ) =b/c (i)
Cos (θ) = b/c (ii)
So, from equation (i) and (ii), we have
Sin (900 – θ) = Cos (θ)
Similarly, the remaining ratios are obtained as
Cos (900 – θ) = Sin (θ)
Tan (900 – θ) = Cot (θ)
Cot (900 – θ) = Tan (θ)
Cosec (900 – θ) = Sec (θ)
Sec (900 – θ) = Cosec (θ)
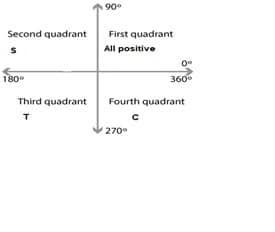
Signs of Trigonometric Functions in Different Quadrants:
The signs of different trigonometric functions are different in different quadrants depending upon the terminal side of the angle θ. To remember the signs of these trigonometric ratios in different quadrants just remember that all the ratios are positive in the first quadrant because x > 0 and y > 0. For the other three quadrants just remember the letters in a sequence S T C. S is used for Sine and its inverse Cosec, T is used for Tan and its inverse Cot and C is used for Cos and its inverse Sec for second, third and fourth quadrants respectively. Below given figure 6 provides a very good description of these signs.
Figure 6:
Example 5: Find the other values of trigonometric ratios, if tan θ = 1 where θ lies in the first quadrant.
Solution: We know that tan θ = 1 = y/x (From Table 2)
Which implies that y = 1 and x = 1
Hence by applying Pythagoras theorem, we get the value of radius (r) as:
r2 = x2 + y2,
putting the values of x and y, we get
r2 = 1+1 ⇒ r2 = 2 ⇒ r =√2
Therefore the remaining trigonometric ratios are
Sin θ =y/r = 1/√2
Cos θ =x/r = 1/√2
Sin θ = y/x = 1
Cosec θ = r/y = √2
Sec θ = r/x = √2
Note: In the similar way the values of trigonometric ratios of 00, 900, 1800, 2700 and 3600 can be calculated.
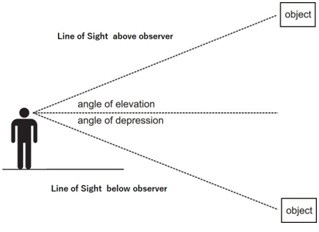
Angle of Elevation and Depression
From the title of the topic it may seem a difficult one but the concepts of this topic are fairly easy and can be easily understood from the figure 7 which can be seen below. But first we define the two angles as: The angle of elevation is an angle formed by a horizontal line and the line of sight to an object that is above the horizontal line. The angle of depression is an angle formed by a horizontal line and the line of sight to an object that is below the horizontal line.
Some real life problems involving the concepts of angle of elevation and the angle of depression
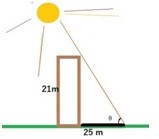
Example 6: A building that is 21 meters tall casts a shadow of 25 meters long. Find the angle of elevation of the sun to the nearest degree.
Solution: From the given data and looking at the figure of the problem it is clear that we need to use the Tan θ =Perp/Base
Here we have Perp = 21 m and Base = 25 m. So using these values we get
Tan θ = 21/25 ⇒ θ = Tan-1 21/25 ⇒ θ = 40 degree (Approximately)
Example 7: A Police helicopter is flying at 800 feet. A Stolen car is sighted at an angle of depression of 720. Find the distance of the stolen car, to the nearest foot, from a point directly below the helicopter.
Solution: From the given data and looking at the figure of the problem it is clear that we need to use the Tan θ =Perp/Base . Here it is worth mentioning that because the given angle of depression (720) is actually an example of the two alternate angles between the parallel lines. This means that the angle of elevation from ground is also 720 and thus the solution is obtained as
Tan 72 =800/d ⇒ d = 800/Tan72
d=800/3.077768 ⇒ d = 260 ft
Example 8: The angle of elevation of the top of the cliff is 300. Walking 210 meters from the point towards the cliff, the angle of elevation becomes 450. Find the height of the cliff.
Solution: From the figure it can be observed that the distance DC is 210 meters and the distance CB is x meters. Thus using the Tan θ = Perp/Base twice for the two triangles at hands and equating the two obtained equations we get.
For Triangle ADB
Tan θ = Perp/Base ⇒ Tan 300 =h/210+x
1/√3=h/210+x ⇒ x = √3 h-210 ( i)
For Triangle ACB
Tan θ =Perp/Base ⇒ Tan 450 =h/x
1=h/x ⇒ x =h eq(ii)
Equating equation (i) and (ii), we get.
h = √3 h-210 ⇒ 210 =√3 h+h
210 =h(√3-1) ⇒ h = 210/√3-1 meters.