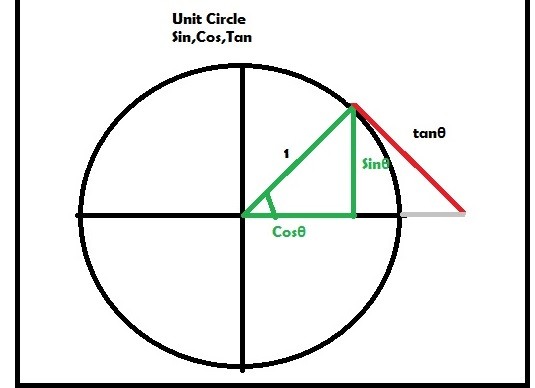
The unit circle is a circle of radius one suspended on any point on the circle’s circumference. The unit circle is used explicitly in trigonometry and is centered at the origin of a Cartesian plane. S1 denotes it because of its one-dimensional structure.
The point to be noted here is that all the trigonometric functions values depend on the unit circle. The interior of the unit circle is known as a unit disk. The word ‘’distance’’ can also describe the nature and the structure of the unit circles. Learn more about Trig identities to clear all the basic knowledge of Trigonometry.
Interactive unit circle
The interactive unit circle connects the trigonometric functions tangent, cosine, and sine and the unit circle. The unit circle is a circle of radius one suspended in a particular quadrant of the coordinate system. The radius of a unit circle can be taken at any point at the perimeter of the circle.
It forms a right-angled triangle. The angle between this unit circle will be represented by angle θ To change a grade, simply click and drag the two control points. This unit circle has three functions.
- Cosine
- Sine
- Tangent
The interaction between this unit circle and its corresponding functions is known as interactive unit circles. Before heading further, let’s first discuss some simple terminologies.
Sine, Cosine and Tangent
- Cosine
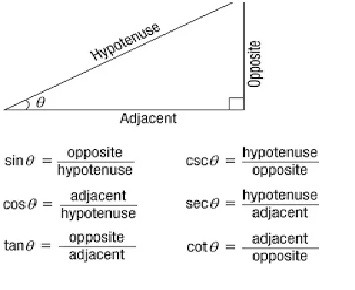
In a right-angled triangle, the ratio between base and hypotenuse is known as cosineθ. It is the most crucial trigonometric function of all. Mathematically, cosine is obtained by dividing the base of a right-angled triangle with its hypotenuse.
Cosine = Base/Hyp
- Secant
The reciprocal of cosine is also used in some triangles. It is known as secantθ and is used in various numerical calculations. It is calculated by reciprocating cosineθ .
Secant=1/cosine
2. Sine
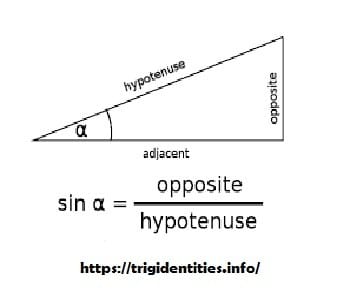
Second and another fundamental trigonometric function is sineθ. Mathematically sineθ is calculated by dividing the perpendicular of a right-angled triangle with its hypotenuse.
Hence we can calculate the length or the angle of any structure with the above relation’s help.
Sineθ = Perpendicular/Hypotenuse
- Cosecant As of cosine, the reciprocal of sineθ is known as cosecantθ. It is calculated by reciprocating sine or simply dividing it by 1.
Cosecantθ=1/sinθ
3. Tangent
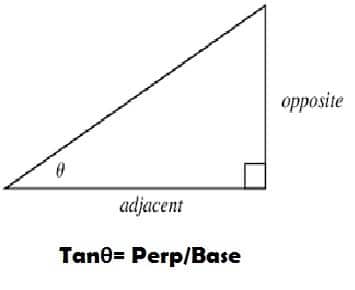
Third and another fundamental trigonometric function is known as tangent . As per sineθ and cosineθ, it is also obtained by a right-angled triangle. By dividing the perpendicular of a triangle with its base, we can easily calculate the value of tangentθ .
The mathematical formula of tangentθ is:
Tangθ= Perp/Base
- Cot
The reciprocal of Tangentθ is known as cotθ . The value of cot can be calculated by reciprocating the value of tangent . The mathematical form of this equation is as stated below:
Cotθ=1/Tangθ
So, all the equations and the trigonometric functions can be understood by the following graph