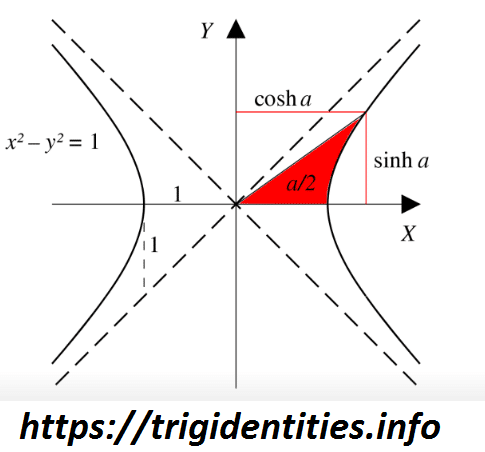
Hyperbolic Trig Identities is like trigonometric identities yet may contrast to it in specific terms. The fundamental hyperbolic functions are hyperbola sin and hyperbola cosine from which the other trigonometric functions are inferred. You can easily explore many other Trig Identities on this website.
So here we have given a Hyperbola diagram along these lines giving you thought regarding the places of sine, cosine, and so on.
Various Essential Hyperbolic Trig Identities
Introduction
- x and y are independent variables.
- e is the base of the natural logarithm.
- d is the differential operator.
- int is the integral symbol.
- C is the constant of integration.
Hyperbolic Trig Identities |
|
| sinh x = (ex – e–x)/2 | Equation 1 |
| cosh x = (ex + e–x)/2 | Equation 2 |
| sech x = 1/cosh x | Equation 3 |
| csch x = 1/sinh x | Equation 4 |
| tanh x = sinh x/cosh x | Equation 5 |
| coth x = 1/tanh x | Equation 6 |
| cosh2 x – sinh2 x = 1 | Equation 7 |
| tanh2 x + sech2 x = 1 | Equation 8 |
| coth2 x – csch2 x = 1 | Equation 9 |
| sinh (x + y) = sinh x cosh y + cosh x sinh y | Equation 10 |
| sinh (x – y) = sinh x cosh y – cosh x sinh y | Equation 11 |
| cosh (x + y) = cosh x cosh y + sinh x sinh y | Equation 12 |
| cosh (x – y) = cosh x cosh y – sinh x sinh y | Equation 13 |
| sinh2 x = [-1 + cosh (2 x)]/2 | Equation 14 |
| sinh (2 x) = 2 sinh x cosh x | Equation 15 |
| cosh2 x = [1 + cosh (2 x)]/2 | Equation 16 |
| cosh (2 x) = cosh2 x + sinh2 x | Equation 17 |
| arcsinh x = ln [x + (x2 + 1)1/2] | Equation 18 |
| arccosh x = ln [x + (x2 – 1)1/2] | Equation 19 |
| arctanh x = (1/2) ln [(1 + x)/(1 – x)] | Equation 20 |
| arccoth x = (1/2) ln [(x + 1)/(x – 1)] | Equation 21 |
| arcsech x = ln [[1 + (1 – x2)1/2]/x] | Equation 22 |
| arccsch x = ln [[1 + (1 + x2)1/2]/|x|] | Equation 23 |
| tanh (2 x) = 2 tanh x/(1 + tanh2 x) | Equation 24 |
| coth x – tanh x = 2 csch (2 x) | Equation 25 |
| coth x + tanh x = 2 coth (2 x) | Equation 26 |
| (d/dx) sinh x = cosh x | Equation 27 |
| (d/dx) cosh x = sinh x | Equation 28 |
| (d/dx) tanh x = sech2 x | Equation 29 |
| (d/dx) coth x = -csch2 x | Equation 30 |
| (d/dx) sech x = -sech x tanh x | Equation 31 |
| (d/dx) csch x = -csch x coth x | Equation 32 |
| (d/dx) arcsinh x = 1/(x2 + 1)1/2 | Equation 33 |
| (d/dx) arccosh x = 1/(x2 – 1)1/2 | Equation 34 |
| (d/dx) arctanh x = 1/(1 – x2) | Equation 35 |
| (d/dx) arccoth x = 1/(1 – x2) | Equation 36 |
| (d/dx) arcsech x = -1/[x (1 – x2)1/2] | Equation 37 |
| (d/dx) arccsch x = -1/[|x| (1 + x2)1/2] | Equation 38 |
| Integrals. | |
| int cosh x dx = sinh x + C | Equation 39 |
| int sinh x dx = cosh x + C | Equation 40 |
| int sech2 x dx = tanh x + C | Equation 41 |
| int csch2 x dx = -coth x + C | Equation 42 |
| int sech x tanh x dx = -sech x + C | Equation 43 |
| int csch x coth x dx = -csch x + C | Equation 44 |
| int dx/(x2 + 1)1/2 = arcsinh x + C | Equation 45 |
| int dx/(x2 – 1)1/2 = arccosh x + C | Equation 46 |
| int dx/(1 – x2) = arctanh x + C | Equation 47 |
| int dx/(1 – x2) = arccoth x + C | Equation 48 |
| int dx/[x (1 – x2)1/2] = -arcsech x + C | Equation 49 |
| int dx/[|x| (1 + x2)1/2] = -arccsch x + C | Equation 50 |