Basic Trig Identities

The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variables. So, these trig identities portray certain functions of at least one angle (it could be more angles). It is identified with a unit circle where the connection between the lines and angles in a Cartesian plane. Today in this article we are going to provide you with the table comprising of a lot of basic trig identities which can be used from the essential trigonometric functions.

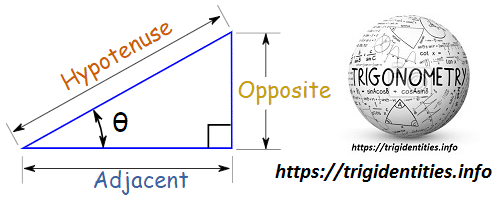
Right Triangle

The Trigonometric Identities or Trig Identities are equations that are true for Right Angled Triangles. (If it is not a Right-Angled Triangle go to the Triangle Identities page.)

Each and every side of a right triangle has a name

• Adjacent is always very next to the Theta θ or Angle
• And Opposite is always opposite the Theta θ or Angle

As a total a triangle has 6 basic elements i.e. 3 sides & 3 angles. Here are the names of 3 sides of a triangle! Learn more about Trigonometry.

• Hypotenuse
• Adjacent
• Opposite

Basic Trig Functions Sine, Cosine and Tangent

The three main functions in trigonometry are

• Sine
• Cosine
• Tangent

You can easily obtain the above-mentioned trigonometric functions by simply length of one side divided by another

For a right triangle with an angle θ:

Sine Function	sin(θ) = Opposite / Hypotenuse
Cosine Function:	cos(θ) = Adjacent / Hypotenuse
Tangent Function:	tan(θ) = Opposite / Adjacent

We can obtain Tangent θ simply by dividing Sine by Cosine we get:

sin(θ)/cos(θ) = Opposite/Hypotenuse / Adjacent/Hypotenuse = Opposite/Adjacent = tan(θ)

So we can say:

tan(θ) = sin(θ)/cos(θ)

That is our first Trigonometric Identity.

Cosecant, Secant and Cotangent

Cosecant Function:	csc(θ) = Hypotenuse / Opposite
Secant Function:	sec(θ) = Hypotenuse / Adjacent
Cotangent Function:	cot(θ) = Adjacent / Opposite

Solved Example: when Opposite = 2 and Hypotenuse = 4 then

sin(θ) = 2/4, and csc(θ) = 4/2

Because of all that we can say:

sin(θ) = 1/csc(θ)

cos(θ) = 1/sec(θ)

tan(θ) = 1/cot(θ)

And the other way around:

csc(θ) = 1/sin(θ)

sec(θ) = 1/cos(θ)

cot(θ) = 1/tan(θ)

And we also have:

cot(θ) = cos(θ)/sin(θ)

Definition of Pythagoras’ Theorem

Pythagoras’ Theorem

“For any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”

a2 + b2 = c2

The key Pythagorean Trigonometric identity are:

sin²(t) + cos²(t) = 1

tan²(t) + 1 = sec²(t)

1 + cot²(t) = csc²(t)

So, from this recipe, we can infer the equations for different capacities additionally: Learn more about Pythagoras Trig Identities.

Dividing through by c² gives

a^2/c² + b^2/c² = c^2/c²

This can be simplified to:

(a/c)² + (b/c)² = 1

Now, a/c is Opposite / Hypotenuse, which is sin(θ)

And b/c is Adjacent / Hypotenuse, which is cos(θ)

So (a/c)² + (b/c)² = 1 can also be written:

sin² θ + cos² θ = 1

Note:

• sin² θ means to find the sine of θ, then square the result, and
• sin θ² means to square θ, then do the sine function

Solve Pythagoras Example:  32°

Using 4 decimal places only:

• sin(32°) = 0.5299…
• cos(32°) = 0.8480…

Now let’s calculate sin² θ + cos² θ:

0.5299² + 0.8480²
= 0.2808… + 0.7191…
= 0.9999…

Related identities include:

sin² θ = 1 − cos² θ
cos² θ = 1 − sin² θ
tan² θ + 1 = sec² θ
tan² θ = sec² θ − 1
cot² θ + 1 = csc² θ
cot² θ = csc² θ − 1

Summary of Basic Trig Identities

Basic Trig Identities
tan x = sin x/cos x	Equation 1
cot x = cos x/sin x	Equation 2
sec x = 1/cos x	Equation 3
csc x = 1/sin x	Equation 4
cot x = 1/tan x	Equation 5
sin2 x + cos2 x = 1	Equation 6
tan2 x + 1 = sec2 x	Equation 7
1 + cot2 x = csc2 x	Equation 8
cos (x +- y) = cos x cos y -+ sin x sin y	Equation 9
sin (x +- y) = sin x cos y +- cos x sin y	Equation 10
cos (-x) = cos x	Equation 11
cos (pi/2 – x) = sin x	Equation 12
cos (2 x) = cos2 x – sin2 x = 2 cos2 x – 1 = 1 – 2 sin2 x	Equation 13
cos (x/2) = +-[(1/2) (1 + cos x)]1/2	Equation 14
sin (-x) = -sin x	Equation 15
sin (pi/2 – x) = cos x	Equation 16
sin (2 x) = 2 sin x cos x	Equation 17
tan (x +- y) = (tan x +- tan y)/(1 -+ tan x tan y)	Equation 18
tan (-x) = -tan x	Equation 19
tan (2 x) = 2 tan x/(1 – tan2 x)	Equation 20
tan (x/2) = sin x/(1 + cos x)	Equation 21
cos (pi +- x) = -cos x	Equation 22
sin (pi +- x) = -+sin x	Equation 23
tan (pi +- x) = +-tan x	Equation 24
Derivatives.
(d/dx) sin x = cos x	Equation 25
(d/dx) cos x = -sin x	Equation 26
(d/dx) tan x = sec2 x	Equation 27
(d/dx) cot x = -csc2 x	Equation 28
(d/dx) sec x = sec x tan x	Equation 29
(d/dx) csc x = -csc x cot x	Equation 30
Integrals.
int sin x dx = -cos x + C	Equation 31
int cos x dx = sin x + C	Equation 32
int tan x dx = -ln |cos x| + C	Equation 33
int cot x dx = ln |sin x| + C	Equation 34
int sec x dx = ln |sec x + tan x| + C	Equation 35
int csc x dx = -ln |csc x + cot x| + C	Equation 36